打印菱形以及斐波纳契数列的几种解法介绍
本篇文章是对打印菱形及斐波纳契数列的几种解法进行了详细的分析介绍,需要的朋友参考下
1、编写程序,打印*菱形
推出第i行要打印的空白个数及*号个数,用for循环依次打印各行
#include<stdio.h>
//总共要打印2*n-1行,逐行打印
void print1(int n)
{
int i,j;
for(i=1;i<=n;i++){//打印1至n行
for(j=1;j<=n-i;j++)//打印n-i个空格
printf(" ");
for(j=1;j<=2*i-1;j++)//打印2*i-1个*号
printf("*");
printf("\n");
}
for(;i<2*n;i++){//打印n+1至2*n-1行,同(2*n-i)行
for(j=1;j<=n-(2*n-i);j++)
printf(" ");
for(j=1;j<=2*(2*n-i)-1;j++)
printf("*");
printf("\n");
}
}
void main()
{
int n;//n是菱形边上*号的个数
printf("enter n:");
scanf("%d",&n);
print1(n);
}
2、斐波纳契数列(Fibonacci Sequence),又称黄金分割数列,指的是这样一个数列:
1、1、2、3、5、8、13、21、……在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n>=2,n∈N*).编写程序,输出F(20)的值。
这里给出四种不同的解法,注意递归和改进的递归效率上有很大区别。
#include<stdio.h>
#include<math.h>
#include<time.h>
#define MAX 100
//递归
int f1(int n)
{
if(n==1 || n==0)
return 1;
return f1(n-1)+f1(n-2);
}
//改进版的递归,去除重复计算
int f2(int n)
{
//保存中间结果的数组
static result[MAX]={1,1};
if(n==1 || n==0)
return 1;
if(result[n-1] == 0)
result[n-1]=f2(n-1);
if(result[n-2] == 0)
result[n-2]=f2(n-2);
return result[n-1]+result[n-2];
}
//用数组保存中间结果(来自陈孝杰)
int f3(int n)
{
int a[MAX],i;
a[1]=1;
a[0]=1;
for(i=2;i<=n;i++)
a[i]=a[i-1]+a[i-2];
return a[n];
}
//迭代
int f4(int n)
{
int i=2,a=1,b=1,sum=1;
while(i<=n){
sum=a+b;
a=b;
b=sum;
i++;
}
return sum;
}
void main()
{
long start,end;
start=clock();
printf("f(40)==%d\n",f1(40));
end=clock();
printf("用时:%d ms\n",end-start);
start=clock();
printf("f(40)==%d\n",f2(40));
end=clock();
printf("用时:%d ms\n",end-start);
start=clock();
printf("f(20)==%d\n",f3(20));
end=clock();
printf("用时:%d ms\n",end-start);
start=clock();
printf("f(20)==%d\n",f4(20));
end=clock();
printf("用时:%d ms\n",end-start);
}
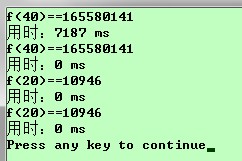
运行结果:
推出第i行要打印的空白个数及*号个数,用for循环依次打印各行
代码如下:
#include<stdio.h>
//总共要打印2*n-1行,逐行打印
void print1(int n)
{
int i,j;
for(i=1;i<=n;i++){//打印1至n行
for(j=1;j<=n-i;j++)//打印n-i个空格
printf(" ");
for(j=1;j<=2*i-1;j++)//打印2*i-1个*号
printf("*");
printf("\n");
}
for(;i<2*n;i++){//打印n+1至2*n-1行,同(2*n-i)行
for(j=1;j<=n-(2*n-i);j++)
printf(" ");
for(j=1;j<=2*(2*n-i)-1;j++)
printf("*");
printf("\n");
}
}
void main()
{
int n;//n是菱形边上*号的个数
printf("enter n:");
scanf("%d",&n);
print1(n);
}
2、斐波纳契数列(Fibonacci Sequence),又称黄金分割数列,指的是这样一个数列:
1、1、2、3、5、8、13、21、……在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n>=2,n∈N*).编写程序,输出F(20)的值。
这里给出四种不同的解法,注意递归和改进的递归效率上有很大区别。
代码如下:
#include<stdio.h>
#include<math.h>
#include<time.h>
#define MAX 100
//递归
int f1(int n)
{
if(n==1 || n==0)
return 1;
return f1(n-1)+f1(n-2);
}
//改进版的递归,去除重复计算
int f2(int n)
{
//保存中间结果的数组
static result[MAX]={1,1};
if(n==1 || n==0)
return 1;
if(result[n-1] == 0)
result[n-1]=f2(n-1);
if(result[n-2] == 0)
result[n-2]=f2(n-2);
return result[n-1]+result[n-2];
}
//用数组保存中间结果(来自陈孝杰)
int f3(int n)
{
int a[MAX],i;
a[1]=1;
a[0]=1;
for(i=2;i<=n;i++)
a[i]=a[i-1]+a[i-2];
return a[n];
}
//迭代
int f4(int n)
{
int i=2,a=1,b=1,sum=1;
while(i<=n){
sum=a+b;
a=b;
b=sum;
i++;
}
return sum;
}
void main()
{
long start,end;
start=clock();
printf("f(40)==%d\n",f1(40));
end=clock();
printf("用时:%d ms\n",end-start);
start=clock();
printf("f(40)==%d\n",f2(40));
end=clock();
printf("用时:%d ms\n",end-start);
start=clock();
printf("f(20)==%d\n",f3(20));
end=clock();
printf("用时:%d ms\n",end-start);
start=clock();
printf("f(20)==%d\n",f4(20));
end=clock();
printf("用时:%d ms\n",end-start);
}
运行结果:

精彩图集
精彩文章





